Many Phase Masks Create a General Transformation! (SLM series)

So far, we’ve discussed what can be achieved by controlling the phase in a single plane using an SLM. Sometimes, however, we want to perform a more complex task, building an optical system that implements a general transformation, such that a given set of inputs is mapped to a corresponding set of outputs. This capability can be useful, for example, in multiplexing multiple communication channels into different modes of a multimode fiber, known as SDM, or in implementing computational tasks using optics.

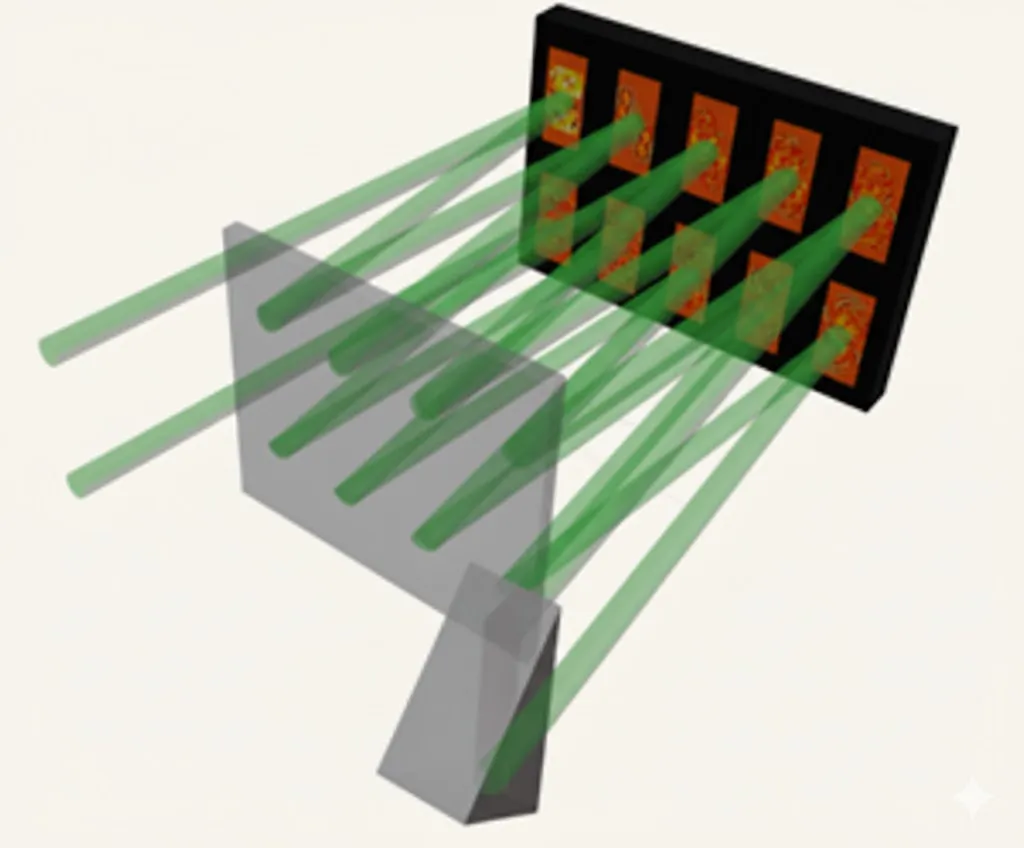
It turns out that for such a task, a single phase mask is usually not enough. Instead, we can use a sequence of several phase masks, allowing the light to diffract between one mask and the next. The masks provide the required phase shifts, diffraction enables mixing of the light, and together they create the desired transformation. In practice, the same SLM is often used to implement multiple planes, by reflecting the light off different regions of the device in a highly controlled manner, see illustration.

The algorithm used to determine the appropriate phase masks is called wavefront matching, and it can be viewed as a generalization of the Gerchberg–Saxton algorithm discussed in the previous article. At each step of the algorithm, all inputs and outputs are propagated to a specific plane, and the phase differences between them are examined. The phase applied at that plane is chosen as a certain average of these phase differences. Repeating this process for each intermediate plane gradually leads to a solution in which every input is mapped to its desired output.

Although there are many additional techniques and applications for SLMs, we will conclude our SLM series here for now. If there are other topics you would like us to cover, write to us, and we’ll do our best to explore them in the future.