Phase Creates an Image (SLM series)

In this post, we’ll demonstrate an algorithm that uses only an SLM to control the phase of the field, and thereby generate any desired image in the far field. The algorithm is named after Gerchberg and Saxton, and its simplest version is a direct implementation of the principle discussed in the previous post.

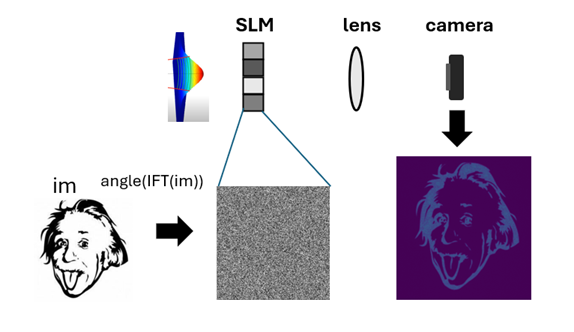
Previously, we saw that in the far field of an image, most of the information is contained in the phases. Therefore, if we want a camera to display an image of Einstein, we can place an SLM in the far field and load onto it the phases obtained from the Fourier transform of Einstein’s image. Although the laser illuminating the SLM will typically have a Gaussian profile, as we learned, phase is more important than amplitude. This simple method already works quite well (see illustration below), but we can do even better!

‍

The full algorithm performs repeated iterations of forward and inverse Fourier transforms between the SLM plane and the camera plane, while enforcing constraints at each step. In the camera plane, the algorithm forces the amplitude to match the desired image, and in the SLM plane, it forces the amplitude to match the given laser profile. In the field of cold atom control, where it is crucial to generate a highly uniform array of laser spots, many extensions of this algorithm have been developed to improve image quality and accelerate convergence, but the core principle remains the same.

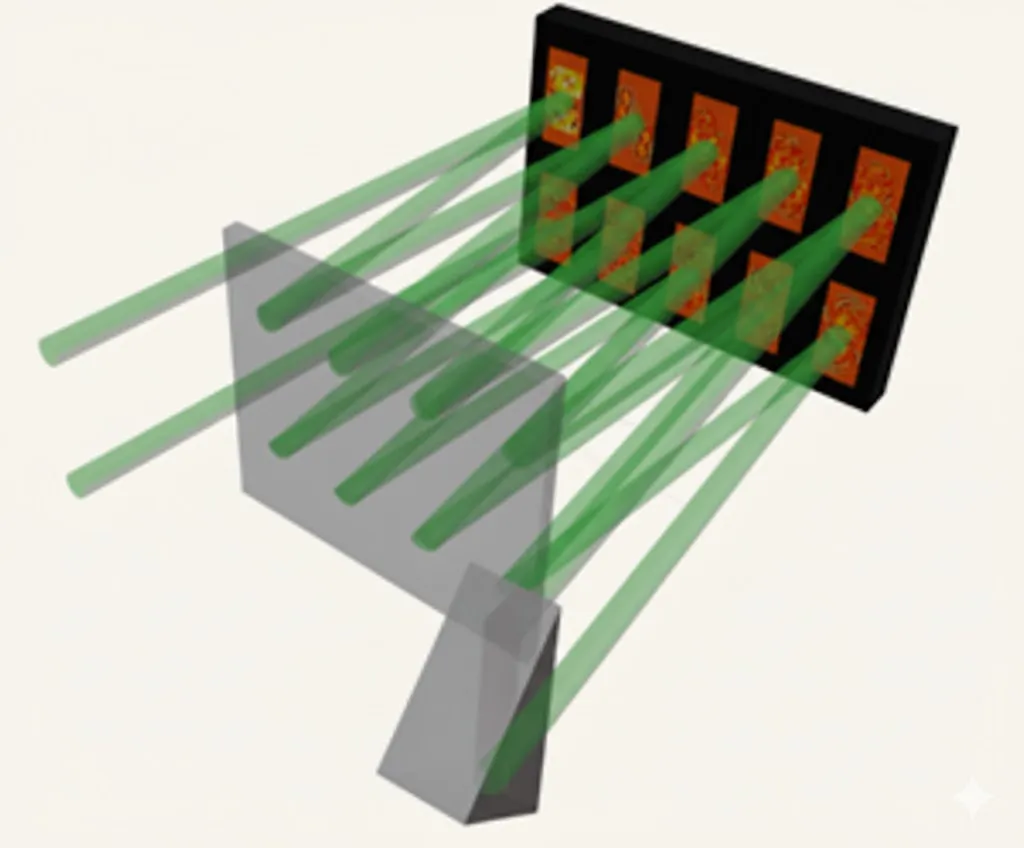
If a single SLM can achieve all this, imagine what an entire array of SLMs could do. We’ll explore that and more in our next article!